Diffie-Hellman: Unterschied zwischen den Versionen
Aus Byte-Welt Wiki
Zur Navigation springenZur Suche springenK |
K (→Ablauf) |
||
| Zeile 4: | Zeile 4: | ||
==Ablauf== | ==Ablauf== | ||
# A und B erzeugen sich einen Wert a bzw. b, diesen Wert behalten sie immer bei sich und versenden ihn nie. Dieser ist ähnlich einem [[geheimen Schlüssel]]. | # A und B erzeugen sich einen Wert a bzw. b, diesen Wert behalten sie immer bei sich und versenden ihn nie. Dieser ist ähnlich einem [[geheimen Schlüssel]]. | ||
| − | # A sendet an B eine [[Primzahl]] p, einen Wert g, außerdem das Ergebnis '''E<sub>A</sub>''' der Rechnung [[ | + | # A sendet an B eine [[Primzahl]] p, einen Wert g, außerdem das Ergebnis '''E<sub>A</sub>''' der Rechnung [[Datei:latex001.gif]]. Diese Daten werden unverschlüsselt übertragen und somit auch für andere Personen lesbar. |
| − | # B berechnet mit den empfangenen Werten und seiner Zufallszahl einen Wert '''E<sub>B</sub>''' und sendet ihn A, | + | # B berechnet mit den empfangenen Werten und seiner Zufallszahl einen Wert '''E<sub>B</sub>''' und sendet ihn A, [[Datei:latex002.gif]]. |
| − | # Anschließend berechnen A und B mit dem empfangenen errechneten Wert des anderen den Sitzungsschlüssel, mit dem alle weiteren Daten verschlüsselt werden. Für A errechnet sich der Schlüssel | + | # Anschließend berechnen A und B mit dem empfangenen errechneten Wert des anderen den Sitzungsschlüssel, mit dem alle weiteren Daten verschlüsselt werden. Für A errechnet sich der Schlüssel [[Datei:latex003.gif]]. |
==Vorteil== | ==Vorteil== | ||
Aktuelle Version vom 4. November 2018, 16:44 Uhr
Das Diffie-Hellman-Verfahren ist das erste veröffentlichte Schlüsselaustauschprotokoll (1976) nach dem Public Key Verfahren.
Inhaltsverzeichnis
Ablauf
- A und B erzeugen sich einen Wert a bzw. b, diesen Wert behalten sie immer bei sich und versenden ihn nie. Dieser ist ähnlich einem geheimen Schlüssel.
- A sendet an B eine Primzahl p, einen Wert g, außerdem das Ergebnis EA der Rechnung
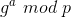. Diese Daten werden unverschlüsselt übertragen und somit auch für andere Personen lesbar. - B berechnet mit den empfangenen Werten und seiner Zufallszahl einen Wert EB und sendet ihn A,
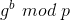. - Anschließend berechnen A und B mit dem empfangenen errechneten Wert des anderen den Sitzungsschlüssel, mit dem alle weiteren Daten verschlüsselt werden. Für A errechnet sich der Schlüssel
.
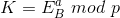Vorteil
Bisher gilt das Verfahren als sicher, da es keine schnellen Verfahren zur Berechnung der Schlüssel existieren. Dieses Verfahren ist mit dem Diskreter-Logarithmus-Problem eng verwandt.
Nachteil/Schwächen
Ein Nachteil des Verfahrens ist der Man-in-the-Middle-Angriff, hier kann sich jemand zwischen A und B setzen und sich so die Daten von A entschlüssel und anschließend an B senden bzw. umgekehrt. Damit dies nicht mehr vorhanden ist gibt es die Erweiterung des Diffie-Hellman-Verfahrens
